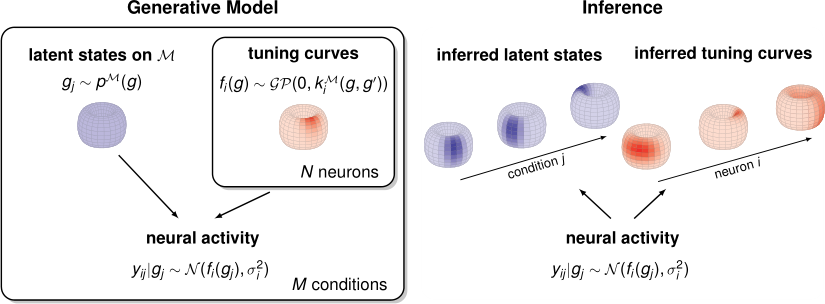
A common problem in neuroscience is to elucidate the collective neural representations of behaviorally important variables such as head direction, spatial location, upcoming movements, or mental spatial transformations. Often, these latent variables are internal constructs not directly accessible to the experimenter. Here, we propose a new probabilistic latent variable model to simultaneously identify the latent state and the way each neuron contributes to its representation in an unsupervised way. In contrast to previous models which assume Euclidean latent spaces, we embrace the fact that latent states often belong to symmetric manifolds such as spheres, tori, or rotation groups of various dimensions. We therefore propose the manifold Gaussian process latent variable model (mGPLVM), where neural responses arise from (i) a shared latent variable living on a specific manifold, and (ii) a set of non-parametric tuning curves determining how each neuron contributes to the representation. Cross-validated comparisons of models with different topologies can be used to distinguish between candidate manifolds, and variational inference enables quantification of uncertainty. We demonstrate the validity of the approach on several synthetic datasets, as well as on calcium recordings from the ellipsoid body of Drosophila melanogaster and extracellular recordings from the mouse anteriodorsal thalamic nucleus. These circuits are both known to encode head direction, and mGPLVM correctly recovers the ring topology expected from neural populations representing a single angular variable.